Quick Way To Remember The Unit Circle: Mastering Trigonometry With Ease

Read Time:3 Minute, 10 Second

Trigonometry can be a challenging subject, but mastering the unit circle is a key step towards understanding the relationships between angles and trigonometric functions.

The unit circle chart is a powerful tool that simplifies complex calculations and makes trigonometry more accessible.

In this guide, we will explore a quick and effective method to remember the unit circle, breaking down its components and providing valuable tips to boost your trigonometry skills.

Understanding The Unit Circle Chart

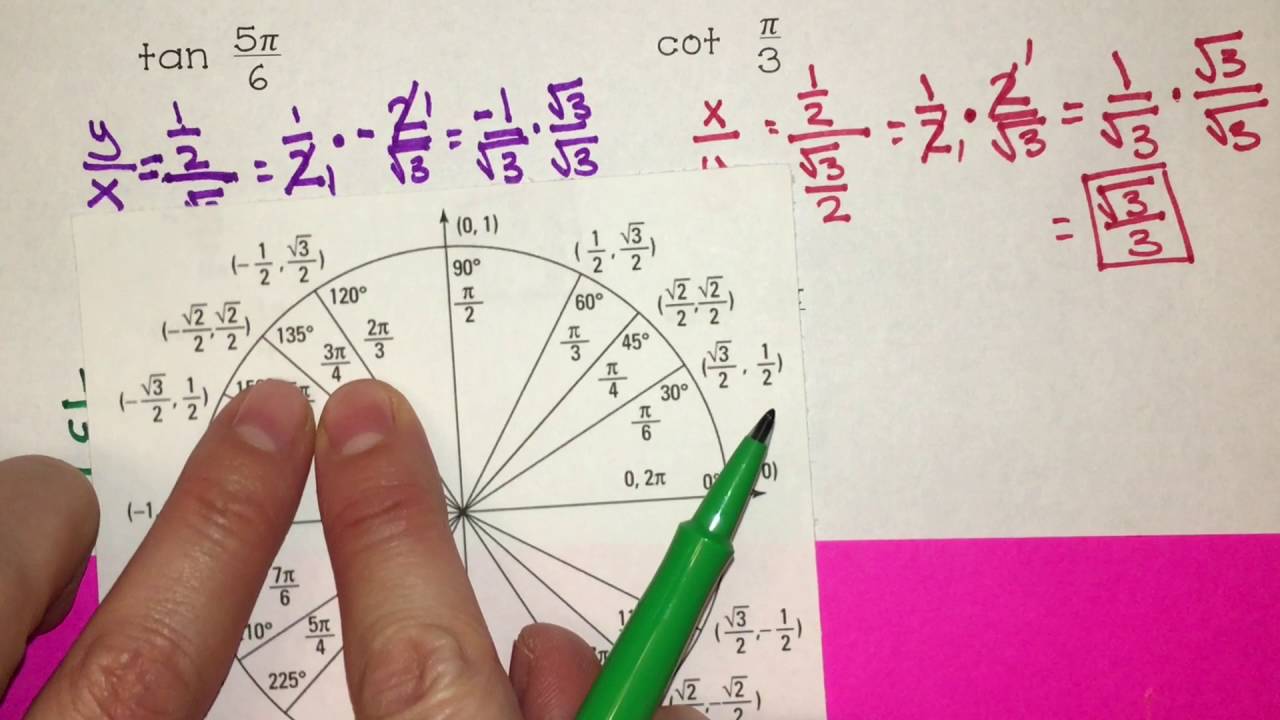
The unit circle is a circle with a radius of 1 unit, centered at the origin of a coordinate plane. It is divided into four quadrants, each representing different combinations of positive and negative values for sine, cosine, and tangent.

The unit circle chart organizes these values in a systematic way, making it an indispensable tool for trigonometric calculations.

Components Of The Unit Circle Chart

Angles in Radians

The unit circle is typically measured in radians, where one full revolution around the circle equals \(2\pi\) radians. Understanding the conversion between degrees and radians is crucial for working with the unit circle chart.

Quadrant Division

The unit circle is divided into four quadrants, labeled I, II, III, and IV, each corresponding to different signs for sine, cosine, and tangent.

Trigonometric Values

The unit circle chart provides the values of sine (\(sin\)), cosine (\(cos\)), and tangent (\(tan\)) for standard angles, typically given in increments of 30 degrees or \(\pi/6\) radians.

Quick Way To Remember The Unit Circle

Visualizing the Quadrants

Start by visualizing the unit circle and its quadrants. Remember that in the first quadrant, all trigonometric values are positive, in the second quadrant, only sine is positive, in the third quadrant, only tangent is positive, and in the fourth quadrant, only cosine is positive.

Memorizing Key Angles

Focus on memorizing the trigonometric values for key angles: 0°, 30°, 45°, 60°, and 90° (or 0, \(\pi/6\), \(\pi/4\), \(\pi/3\), and \(\pi/2\) in radians). These values will serve as the foundation for understanding other angles.

Recall the Special Right Triangles

The unit circle is closely related to special right triangles, specifically the 30-60-90 and 45-45-90 triangles. Understanding these triangles can help you derive trigonometric values quickly.

Use Mnemonics

Create a mnemonic or a phrase to remember the order of trigonometric functions in each quadrant. For example, “All Students Take Calculus” can help you recall the positive functions in each quadrant (All, Sine, Tangent, Cosine).

FAQs – Frequently Asked Questions

What Is The Significance Of The Unit Circle In Trigonometry?

The unit circle serves as a reference for understanding the relationships between angles and trigonometric functions. It simplifies calculations and provides a visual representation of sine, cosine, and tangent values.

How Do I Convert Degrees To Radians For The Unit Circle Chart?

To convert degrees to radians, use the formula \(\text{radians} = \frac{\text{degrees} \times \pi}{180}\). This conversion is essential for working with the unit circle chart in radians.

Can You Provide An Example Of Using The Unit Circle Chart Values?

Certainly, Let’s take the angle of 45 degrees (or \(\pi/4\) radians). In the unit circle, the sine, cosine, and tangent values for this angle are \(\frac{\sqrt{2}}{2}\), \(\frac{\sqrt{2}}{2}\), and 1, respectively.

How Does The Unit Circle Chart Help In Solving Trigonometric Equations?

The unit circle chart provides a quick reference for trigonometric values, making it easier to solve equations involving angles. By understanding the patterns in the chart, you can simplify calculations and identify solutions efficiently.

Conclusion

Mastering the unit circle is a fundamental step in conquering trigonometry. Utilize the unit circle chart, follow the quick memorization tips, and practice regularly to build confidence in working with trigonometric functions. With this knowledge, you’ll be well-equipped to tackle more advanced trigonometry concepts and applications.